Construction d'un problème de minimisation de la consommation d'énergie
Sur la base du modèle de transmission de données de la section précédente, si la puissance de transmission du terminal mobile est P, la consommation d'énergie d'une transmission de données à l'aide de m est P-t. En supposant que le nombre de fois pour un tour de détection de canal à l'aide de m est N, alors un tour de détection de largeur de bande de canal La consommation totale d'énergie pour la mesure et la transmission de données est : Emx=N-E, P - t.
Si le terminal mobile utilise de manière répétée la règle donnée RMB round pour l'application m, alors la séquence de numéros de temps d'arrêt {N, N,,...,N,,...,Ny| et la séquence de consommation totale d'énergie {Ex, Ex,..., générée par le RMB round) ,Ex ,... ,Exy}.où,N. Indique le numéro de l'heure d'arrêt de la roue principale. E est la consommation totale d'énergie lorsque la roue principale s'arrête à N. Lorsque la m-ième roue s'arrête à N, le temps total passé par le terminal mobile est le temps de détection ATx, =T-N, et le temps de transmission t, qui est ATx. t. La quantité de données à transmettre est Q1). La quantité de données à ne pas transmettre dans ce tour Lmx est donc :
Si le terminal mobile obtient la consommation d'énergie moyenne minimale par unité de données après avoir observé le canal en continu N fois, N est le temps d'arrêt optimal. Étant donné que le terminal mobile détecte au moins un
la largeur de bande du sous-canal, de sorte que le temps d'arrêt optimal est N≥1. Le délai de transmission maximal des données à transmettre est Dm. Définissons Z=LDm/T", puis 1≤n≤N≤Z.
D'après le théorème des grands nombres, l'équation (7) converge vers ME[E,]/E[Q 1)-Ly]. Par conséquent, nous construisons un temps d'arrêt 1≤N≤Z pour minimiser ME[Ex]/EL[Q *1)-L]. Cette règle est dérivée du taux de transmission du canal r détecté pendant l'intervalle T, et de la séquence de temps de détection AT, et génère la séquence de consommation d'énergie Ex, la séquence de volume de données à transmettre O, et la séquence de quantité de données qui ne peut pas être transmise L. Ces valeurs de séquence peuvent être obtenues par mesure.
4.2 Solution du problème de la secrétaire pour la minimisation de la consommation d'énergie
Notre objectif est de minimiser la consommation moyenne d'énergie pendant le processus de transmission des données du terminal mobile vers le nuage, c'est-à-dire de choisir le moment où le taux de transmission est le plus élevé pour transmettre les données. Dans cette section, nous appliquerons la règle consistant à laisser partir k candidats et à accepter les meilleurs. Résoudre pour obtenir la valeur optimale de k et prouver que la valeur de k obtenue est la valeur optimale.
Cet article définit V comme le classement absolu des candidats sélectionnés selon la règle consistant à écarter k candidats et à accepter ensuite les meilleurs candidats ; la probabilité que le classement absolu du candidat sélectionné soit r et la taille du pas est s. PN =P(V=r) est la probabilité que le classement absolu du candidat sélectionné soit r à la fin du processus de prise de décision.
Lemma 1. Lorsque 1≤k≤N-1 et k 1≤s≤N, il existe :
Le terminal mobile effectue une détection de canal à chaque période T. Après k détections, lorsqu'il détecte que le taux r à l'instant présent est supérieur à toute valeur de taux précédente, le terminal mobile arrête la détection et envoie des données au nuage. Dans le cas contraire, il continue à détecter. Si le terminal mobile ne transmet pas de données pour les premières Z-1 détections, il doit envoyer des données lorsque le temps de détection atteint le nombre maximum de détections Z. Le terminal mobile continue la détection des canaux et la transmission des données selon cette stratégie, réduisant ainsi la consommation d'énergie pendant la transmission des données. 5 Résultats de la simulation et analyse
Dans cette section, nous menons des expériences de simulation pour comparer la stratégie proposée avec les stratégies de la littérature connexe sous trois aspects : la consommation moyenne d'énergie par unité de données, l'efficacité énergétique et l'efficacité de détection, afin de prouver l'applicabilité de notre stratégie proposée.
L'évanouissement des données pendant la transmission par canal sans fil est un évanouissement à petite échelle, et son modèle d'évanouissement est généralement simulé comme une distribution de Rayleigh et une distribution de Rician. Dans l'expérience, nous avons mené des expériences de simulation dans l'environnement de simulation des deux modèles d'évanouissement, et les valeurs des paramètres expérimentaux sont indiquées dans le tableau 1.
Ce document propose une stratégie de transmission optimale basée sur le problème du secrétaire (OTSSP), fondée sur la théorie de l'arrêt optimal du problème du secrétaire, qui consiste à laisser partir k candidats et à accepter ensuite les meilleurs candidats, et la compare à deux autres stratégies connexes de la littérature. Les deux autres stratégies de comparaison sont les suivantes :
1) Mécanisme "The Sooner The Better" (TSTB) : le terminal mobile envoie des données après avoir détecté le canal pour la première fois ;
2) Stratégie de transmission aléatoire (RTS) : Le terminal mobile choisit au hasard un certain moment pour la transmission des données parmi Z horloges avec un délai de transmission maximal Dm avec une probabilité égale 1/Z.
Afin de tenir compte de facteurs tels que la consommation d'énergie moyenne et le délai de transmission maximal, conformément à la littérature [3], nous fixons dans l'expérience le nombre maximal d'applications de terminal mobile M à s ; le taux de génération de données c à 10×103bps ; et la période de détection de données T à La valeur est de 1s ; le temps de transmission de données r prend la valeur 0,9s ; le délai de transmission de données est D. La valeur est de 10s ; la consommation d'énergie pour la détection de données E est de 1×10J. Dans cette expérience, nous considérons le nombre maximal d'applications M, le taux de génération de données c et le délai de transmission des données D. L'impact sur la consommation moyenne d'énergie par unité de données, l'efficacité de la consommation d'énergie et l'efficacité de la détection est modifié. Le facteur de changement M a une plage de valeurs de 1~10 ; c a une plage de valeurs de 1×103~15 x 10'bps ; D a une plage de valeurs de 1~15s .
5.1 Consommation moyenne d'énergie
La consommation d'énergie moyenne reflète l'énergie consommée par chaque bit de données dans les données transmises avec succès (y compris la consommation d'énergie de détection du canal Ep et la consommation d'énergie de transmission des données Pt).
La figure 2 montre les résultats de la comparaison de la consommation moyenne d'énergie des trois stratégies en fonction de différents changements de M dans le cadre de la distribution de Rayleigh et de la distribution de Rician. La figure 2 montre que la consommation moyenne d'énergie de chaque stratégie de la distribution de Rician est inférieure à la consommation moyenne d'énergie de la stratégie correspondante de la distribution de Rayleigh. À mesure que la valeur M augmente, la consommation moyenne d'énergie de la stratégie OTSSP est la plus faible par rapport aux deux autres stratégies à la même valeur M, l'efficacité énergétique est optimale et le taux de croissance de la consommation moyenne d'énergie est le plus faible ; la stratégie TSTB ne tient pas compte de la consommation d'énergie.
La figure 3 montre les résultats de la comparaison de la consommation moyenne d'énergie des trois stratégies en fonction de différents changements de c dans le cadre de la distribution de Rayleigh et de la distribution de Rician. La valeur moyenne de la consommation d'énergie de la stratégie OTSSP et de la stratégie RTS est affichée sur le côté gauche de l'axe ¥, et la valeur moyenne de la consommation d'énergie de la stratégie TSTB est sur l'axe ¥. Illustration à droite. La figure 3 montre que dans les distributions de Rayleigh et de Rician, lorsque la valeur de c augmente, les valeurs moyennes de consommation d'énergie de la stratégie OTSSP et de la stratégie RTS ne sont pas trop élevées respectivement.
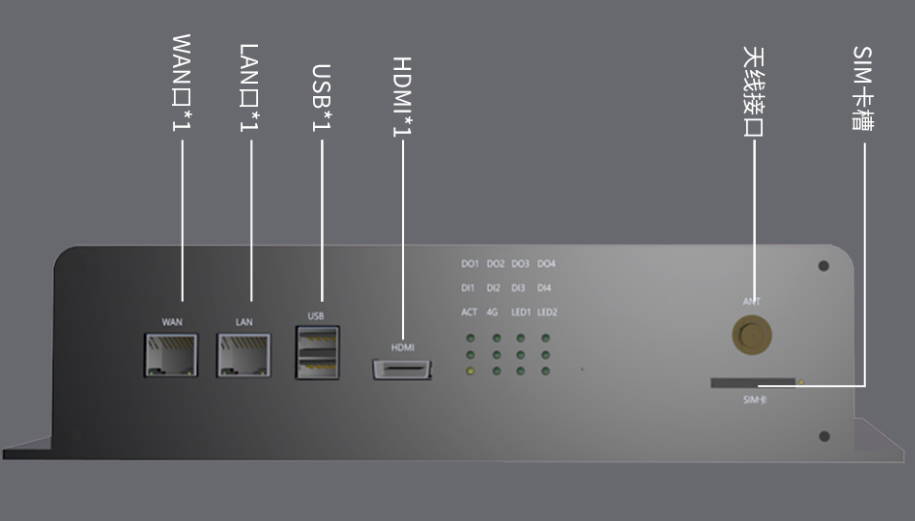
Passerelle IoT
Étant donné que les données sont transmises lorsque les conditions du canal sont bonnes, le taux de transmission des données est supérieur au taux de génération des données et aucune grande quantité de données n'est perdue en raison d'un dépassement du délai de transmission, de sorte que la consommation moyenne d'énergie par unité de données diminue progressivement. L'efficacité de la consommation d'énergie de la stratégie TSTB est nettement inférieure à celle des deux autres stratégies parce que la stratégie TSTB transmet les données au premier moment transmissible. L'état du canal à ce moment-là n'est souvent pas idéal et la quantité de données transmises est faible. Lorsque la quantité de données transmises est égale aux deux autres quantités de données, il faut consommer plus d'énergie.
La figure 4 montre les différentes D selon la distribution de Rayleigh et la distribution de Rician. Résultats de la comparaison de la consommation moyenne d'énergie des trois stratégies en cas de changement. La figure 4 montre que, parmi les deux distributions, la stratégie OTSSP a la consommation d'énergie moyenne la plus faible et la meilleure efficacité énergétique. La stratégie OTSSP et la stratégie RTS sont différentes l'une de l'autre en raison du temps de transmission des données. De même, la valeur moyenne de la consommation d'énergie a tendance à diminuer à mesure que Dm augmente. En effet, lorsque Dm augmente, les données générées ont plus de chances d'être transmises au nuage avant le délai maximal, et l'énergie consommée par unité de données diminue, de sorte que la consommation moyenne d'énergie affiche une tendance à la baisse. Lorsque le délai D est supérieur à 25 secondes, la consommation d'énergie par bit de données est infiniment proche de 0, mais n'est pas égale à 0. À ce moment-là, bien que la consommation d'énergie moyenne soit faible, l'expérience de l'utilisateur n'est pas bonne.
5.2 Efficacité énergétique
Efficacité énergétique ? Reflète l'énergie consommée par unité de temps pendant la transmission des données (y compris le temps T du canal de détection et le temps t de la transmission des données). Plus l'efficacité énergétique est faible, moins la stratégie consomme d'énergie par unité de temps.
La figure 5 montre les résultats de la comparaison de la valeur n de l'efficacité énergétique des trois stratégies lorsque M change dans le cadre d'une distribution de Rayleigh et d'une distribution de Rician. La figure 5 montre que, dans les deux distributions, le nombre maximal d'applications des trois stratégies M et ? Les valeurs montrent une relation de croissance linéaire. La stratégie OTSSP a la valeur n la plus faible et la stratégie TSTB a la valeur n la plus élevée parce qu'elle ne tient pas compte des facteurs énergétiques. Parallèlement, à mesure que la valeur M augmente, la valeur de la stratégie OTSSP croît le plus lentement. Cela montre que lorsqu'une grande quantité de données est transmise simultanément au nuage, le taux de consommation d'énergie de la stratégie OTSSP augmente lentement, donne de meilleurs résultats expérimentaux et jette les bases d'un développement rapide de l'informatique mobile en nuage.
La figure 6 montre les résultats de la comparaison de l'efficacité énergétique n des trois stratégies lorsque c change sous la distribution de Rayleigh et la distribution de Rician. Comme les trois stratégies ne peuvent pas exprimer clairement l'amplitude du changement dans une seule image, la stratégie OTSSP est affichée dans une image séparée ; et ( Dans les images b) et (d), la valeur de l'efficacité de la consommation d'énergie de la stratégie TSTB est affichée sur le côté gauche de l'axe Y¥, et la valeur de l'efficacité de la consommation d'énergie de la stratégie RTS est affichée sur le côté droit de l'axe Y¥. D'après la figure 6
On constate que les valeurs d'efficacité énergétique des trois stratégies dans la distribution de Rician sont meilleures que celles de la distribution de Rayleigh. Lorsque le taux de génération de données c augmente, quelle est la valeur de l'efficacité énergétique de la stratégie OTSSP dans la distribution de Rayleigh ? Les valeurs sont concentrées en 0,0497 ~ 0,05, les valeurs n de la stratégie TSTB sont concentrées en 0,328 ~ 0,332, les valeurs de la stratégie RTS sont concentrées en 0,078 ~ 0,0784 ; dans la distribution de Rician, les valeurs de la stratégie OTSSP sont concentrées en 0,0462 ~ 0,0465 ; les valeurs n de la stratégie TSTB sont concentrées en 0,1842 ~ 0,1846 ; la valeur n de la stratégie RTS est concentrée en 0,0780 ~ 0,0784. En d'autres termes, la stratégie OTSSP proposée dans cet article présente l'efficacité de consommation d'énergie la plus faible, consomme le moins d'énergie par unité de temps et a le meilleur effet d'économie d'énergie. La stratégie orSSP détecte le débit du canal pour les k premières fois, à partir de la première détection, lorsque le débit du canal est supérieur aux k fois précédentes, la détection est arrêtée et les données sont envoyées, ce qui améliore considérablement le débit de transmission des données et l'utilisation de l'énergie.
6 Conclusion
Avec le développement rapide des réseaux mobiles et de l'informatique en nuage mobile, la réduction de la consommation d'énergie des terminaux mobiles et des nuages, l'amélioration de l'utilisation de l'énergie et de l'expérience de l'utilisateur est l'un des problèmes urgents que l'informatique en nuage verte doit résoudre. La couche réseau du processus de transmission des données est étudiée pour réduire la consommation d'énergie de l'informatique en nuage mobile. Cet article est consacré à l'étude du problème de l'optimisation de la consommation d'énergie des terminaux mobiles au cours du processus de transmission des données de l'informatique en nuage mobile. Pendant le processus de transmission des données entre le terminal mobile et le nuage, en raison de la mobilité de l'utilisateur mobile, des changements météorologiques et de l'instabilité de la bande passante du réseau, si le terminal mobile choisit d'envoyer des données au nuage à un moment où l'état du canal est bon et le taux de transmission élevé, il peut réduire une grande partie de la consommation d'énergie et améliorer l'utilisation de l'énergie. La théorie de l'arrêt optimal est un outil efficace pour résoudre le problème du temps d'arrêt maximal et fournit une base pour optimiser la consommation d'énergie des terminaux mobiles lors de la transmission de données. Basé sur le problème du secrétariat dans lequel le classement absolu moyen des candidats sélectionnés est le plus petit, ce document propose de laisser partir k candidats et d'accepter ensuite les meilleurs candidats. Stratégie d'optimisation de la consommation d'énergie. Cet article considère le cas où la transmission des données a un certain retard. Dans la distribution de Rayleigh et la distribution de Rician, en supposant un taux de génération de données constant, un modèle de file d'attente de transmission de données avec des applications multiples et un modèle de minimisation de la consommation moyenne d'énergie par unité de données sont construits. Les résultats de l'expérience de simulation montrent que le système OTSS a été conçu pour minimiser la consommation moyenne d'énergie par unité de données, et qu'il utilise le problème du secrétariat amélioré (la règle qui consiste à laisser partir k candidats et à accepter ceux qui ont les meilleurs résultats) pour résoudre le problème afin de minimiser la consommation moyenne d'énergie par unité de données. Dans l'expérience de simulation, la stratégie OTSSP et la stratégie TSTB proposées dans cet article sont comparées à la stratégie RTS, et l'on constate que la stratégie OTSSP a une consommation d'énergie moyenne plus faible.
Mots-clés : Passerelle pour l'internet des objets